Adjustment for Multiple Comparisons

The overall shipping decision dictates how to adjust alpha and power for multiple comparisons.

Confidence centers the adjustment for multiple comparisons around the idea of a decision rule. In an experiment, it’s the decision to release or not release a new feature that the experiment design should control the risks for. The adjustments vary among metrics, because different types of metrics contribute differently to the decision rule. The adjustments ensure that the observed alpha for the binary decision to ship or not is at most equal to the original alpha. Similarly for power, the observed power level is at least equal to the original power level across repeated experiments.

The Overall Shipping Decision

An important feature of the statistical analysis in Confidence is that the errors that can happen, false positive and false negatives, matter on the experiment level, and not on the individual metric level. In other words, the rates at which these errors happen is over repeated experiments. From a product perspective, false positives and false negatives exist for the decision to ship a feature or not. A false positive is when you ship a feature that truly doesn’t have an effect, and a false negative is when you don’t ship a feature that truly had an effect.

App

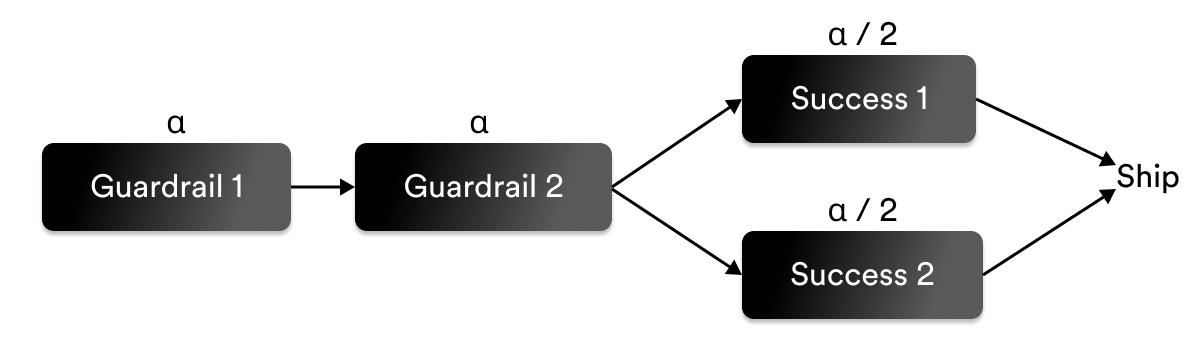
Confidence uses a composite decision rule to produce an overall recommendation for a shipping decision. The results must pass the following for a recommendation to ship:

• at least one success metric has evidence of improvement
• all guardrail metrics show evidence of being within acceptable margins

Alpha needs only to be corrected for the number of success metrics, since the requirement on the guardrail metrics is that they are all simultaneously significant. To properly control the power level for the shipping decision, we need to correct the power level used for each individual metric for the number of guardrail metrics.

The multiple comparison adjustments used are:

• Alpha is adjusted using a Bonferroni correction, where the original alpha is divided by the number of success metrics.
• The power level is adjusted using 1 - (1 - power)/(number of guardrails).

API

The AnalysisPlan object in the stats API contains a decisionRule object that specifies the decision rule, expressed as AND and OR conditions between metrics or groups of metrics. The multiple comparison adjustments aim to control the false positive rate of the decision rule using a general approach that adjusts the false positive rate and the power level used for each individual test. The adjustment depends on each metric’s role within the decision rule and uses ideas of union-intersection and intersection-union testing. See Dmitrienko, Tamhane, and Bretz (2009) for more information about adjustments for these types of tests.

If you specify a decision rule then multiple testing correction is performed according to the rule. If you don’t use a decision rule, a Bonferroni multiple testing correction is used.

The figure shows an example of a decision rule:

References

• A. Dmitrienko, A.C. Tamhane,, and F. Bretz (Eds.) (2009) “Multiple Testing Problems in Pharmaceutical Statistics” (First ed.), Chapman and Hall/CRC.

Related Resources

Analyze Results

Understand decision rules

Statistical Settings

Configure alpha and power

Metrics in Experiments

Configure success and guardrails

Statistical Tests

Understand test types